donde F'(X) es la derivada de f con respecto a x, y donde dx es una variable real adicional (de manera que dy es una función de dos variables x, y dx). La notación es tal que la expresión:
donde la derivada es representada en la notación de Leibniz dy/dx, se mantiene, y es consistente con respecto a la derivada como el cociente de diferenciales.
El significado preciso de las variables dy y dx depende del contexto de aplicación y del nivel de rigor matemático requerido. Según consideraciones matemáticas rigurosas modernas, las notaciones dy y dx son simplemente variables reales y son manipuladas como tales. El dominio de estas variables puede tomar un significado geométrico particular si el diferencial es considerado como una forma diferencial, o significado analítico si el diferencial es considerado como una aproximación lineal al incremento de una función. En aplicaciones físicas, a menudo, se requiere que las variables dx y dy sean sumamente pequeñas (infinitesimales).
Dale a tu cuerpo video macarena:
Pasele a la fuente, subale lugares pipiripi:https://es.wikipedia.org/wiki/Diferencial_de_una_funci%C3%B3n
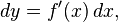
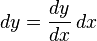
No hay comentarios:
Publicar un comentario